97學年度2nd Semester生物統計學教學大綱

教師：李  炎   學分/每週時數：3/3  上課地點：電腦教室

評分：每週平時測驗累積    課程：教師自編講義

 教學大綱：

第1週：第1章 序  言（生統定義、抽樣方法、）。第2章 統計圖表

第2週：第3章 集中趨勢測定值（Measures of Central Tendency）。分配曲線（Distribution curve）。平均數（mean）。中位數（median）。眾數（mode）。偏態（skew）。變異數（variance）。標準差（Standard deviation）。�Z異係數（coefficient of variance—C.V.）。

第3週：第4章 機   率。第5章 機率分配。超幾何分配、二項分配。Poisson分配。

第4週：常態分配。

第5週：第6章 單1母群體平均數的估計及檢定。中央極限定理。信賴區間（Cofidence Interval-CI）。信賴水準（cofidence level）。

第6週：t分配或學生分配。

第7週：第7章 假設檢定。

第8週：Chi-test、F-test、t-test。

第9週：樣本大小之決定。

第10週：期中考。

第11週：第8章 �O個母群體平均數差的估計與檢定。

第12週：第9章 卡方檢定（Chi-square Test）。

第13週：第10章 母群體變異數的估計與檢定。

第14週：第11章 迴歸（regression）與相關（Correlation）。

第15週：第12章 無母數統計（Nonparametric Methods）。

第16週：實驗設計

第17週：變異數分析

第18週：期末考  

生物統計學重點複習（Biostatistics Overview）

李  炎 編

�謔珚禤ヾG

1.楊志良,2002.生物統計學新論. 藝軒圖書出版社.臺北.

2.張念臺, 2001.是誰將數字變得有意義了？.藝軒圖書出版社.臺北.

3.彭游，吳水丕, 1991. 生物統計學.合記圖書出版社. 4^th edition. 台北.

4.陳凱爾譯. Meehan AM, Warner CB,著. 2001. Excel 在統計學上的應用. 五南圖書出版有限公司. 台北.

5.王文中, 1998. Excel於資料分析與統計學上的應用. 博碩文化. 臺北.

6. HyperStat Online Textbook ：http://davidmlane.com/hyperstat/index.html 。

7. Visual Statistics with Multimedia: An On-Line Textbook ：http://www.visualstatistics.net/Visual%20Statistics%20Multimedia/Outline%20of%20Visual%20Statistics.htm 。

8.. George Mason University, School of Management ：Managerial Statistics
[ Primers and Practice Problems ]   by Dr. Sid Das.

http://mason.gmu.edu/~sdas/stats600/content1.htm 。

第1章 序  言

含義：運用統計方法、研究工具等，從事生命科學的研究---生物統計學

�躑z統計（descriptive statistics）：著重如何收集、整理、描述、分析、及解釋現有數据。

推理統計（inferential statistics）：以部份來推測全體。面對不確定問題，如何下決定。

Types of data：

資料轉換（Data transformation）：

如5人身高為（cm）：176 168 173 180 169；可轉換為1 2 3 4 5；1代表180，2代表176，3代表173，…..。或反過來，1代表168，2代表169，…….。

又如：

群體與抽樣

「母群體」（population）：所研究事物對象之全體。

由於經費、時間、人力、所限，常難以普查（census），故常用抽樣（sampling）。

抽樣：隨機抽樣（random sampling）--又分：

簡單隨機抽樣（Simple random sampling）：群體中每1個體被抽的機會相同。可用隨機亂數表（http://www.ccm.edu/stw/witcookie/npd2rnt.htm ）協助。彩卷中獎號、鈔票號等有時也可用。

分層隨機抽樣（Stratified random sampling）：先將樣本歸類分層（strata），再由各層中隨機抽樣。如健保局調查全民健康情形，抽樣，分1-5、6-10、……歲，各抽幾人。

研究題：設某高中三年級，有男生250人，女生120人，今做身高調查，測男生50人，得平均身高173.5cm，女生30人，平均身高162.3cm，求該校三年級男女生平均身高。

173.5 x 250/370 + 162.3 x 120/370 ＝170.88（cm）

集群隨機抽樣（Cluster random sampling）：將母群體之個體分群，再隨機抽出若干群，並對所抽到各群之個體全面調查。如教育部看不同學校生近視情形。先抽大、中、小�a，抽到之校全面調查。

系統隨機抽樣（Systematic random sampling）：規則地由母群體中每隔一定「距離」抽取1個樣本。

抽樣時亦當考慮：

樣本數大小、放回不放回（含破壞性取樣）、游動樣本（野生動物、魚….等以某區域內所見為準）等問題。

抽樣方式與實驗設計有關。

測驗題：若想瞭解全國小6年級男學生，跑百米的平均時間，將各�鐘狴咱H上�艦哄A抽出10個，再由其中各抽5所小學，每校各抽10人測驗，此抽樣調查方式，是否良好？（若外島�艦咱憬漼魽H…..）2%

討論題：2100全民開講的call in電話來源人，是否隨機？1%

第2章 統計圖表

使資料簡化易懂。

（將Microsoft Excel 打開，點選「工具」欄，再將pull down window拉下，至「增益集」，點選其中「資料分析」項）

做班員基本資料搜集[hight, arm length, ....]。填入Excel Spreadsheet 中（Book1）。

直的為「欄」，橫的為「列」。

1.      用「班員基本資料」中任1項，以Microsoft Excel做次數分配圖表。（見Excel Test-2，Sheet1說明）

2.      用「班員基本資料」中任1項，以Microsoft Excel做1種分析圖。（見Excel Test-2，Sheet2及Chart2說明）

3.      用「班員基本資料」中任1項，以Microsoft Excel做1種分析圖。（見Excel Test-2，Sheet3說明）

由http://www.economics.pomona.edu/statsite/SSP.html 下載免費統計軟體，並熟�堥銌峟p圖表製作（用所收集之資料），列述步驟及結果。3%。

第3章 集中趨勢測定值（Measures of Central Tendency）

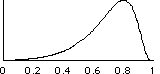
分配曲線（Distribution curve）：

若觀測值很多，將角次觀測值做成直方圖，將各直方圖頂端中心連起，則成1條光滑曲線，稱為分配曲線。

�謔牷Ghttp://www.visualstatistics.net/Visual%20Statistics%20Multimedia/measures_of_central_tendency.htm

平均數（mean）：

母群體平均數=>μ＝ Σx_i/N

式中，Σ為希臘字因sigma的大寫，意為「summation of=>總和」。N為

母群體中之個體數。

樣本平均數=> ＝ Σx_i/n，n為樣本數。

另有幾何、加權、調和、平均數。

中位數（median）：

眾數（mode）：

在1組統計資料中出現次數最多的數值。商業上用的多。1組統計資料中可能沒有眾數或不只1個眾數。有1個眾數的稱為單�腄]unimodal），2個眾數的稱為雙�腄]bimodal），2個以上眾數的稱為多�腄]multimodal）。如社�N流行迷你及迷底�ヾA不可用平均值而生產「迷膝」裝，沒人買。

偏態（skew）：

右偏：mean – median >0

左偏：mean – median <0

Relationships of the Mean, Median, and Mode in Symmetrical and Skewed Distributions

The Theoretical Normal Distribution

資料的差異情況，可由變異數（variance）顯示。母群體變異數，用希臘字母sigma小寫的平方代表, 。

 樣本變異數以S²代表。（M代表mean）
若用樣本變異數代表母群體之 s²,則需用，

（）否則會低估。而此n-1被稱為自由度（degrees of Freedom），以df 或 n, (希臘字母nu)代表。 （http://davidmlane.com/hyperstat/desc_univ.html ）

原因是，樣本變異數會小於母群體變異數（可用1、2、3、4、5、6、7、8及2、3、4、5、6、7兩組數來試求比較之）。只好調小分母以補救。但n>30時可不計。

標準差（Standard deviation）就是�Z異數的平方根。即σ代表母群體標準差，s代表樣本標準差。

�Z異係數（coefficient of variance—C.V.）：標準差除以平均數。

練習：

用Microsoft Excel將Book1中各組數据之平均數、�Z異數、標準差算出。4%。

第4章 機   率                  

在一次實驗中所有可能出現的結果稱為樣本空間（sample space）。以S代表。其中的每1個結果稱為事件（event）。以Ei或Xi代表。

P（A）= S/N（Probability of A = S/N，N為總實驗次數）

有關機率的定理：

1.    互斥事件：P（A or B）= P（A）+ P（B）

2.    非互斥事件：P（A or B）= P（A）+ P（B）－ P（AB）

3.    獨立事件：P（A and B）= P（A）x P（B）

4.    相依事件：P（A and B）= P（A）x P（B∣A）

所謂P（B∣A）為條件機率，情形不一，例：

在同一副撲克牌（共52張）中抽1張，抽出不放回，連2張均為黑桃之機率為：P（A）x P（B∣A）＝ 13/52 x 12/51＝156/2652

又例：

假設查美國人之生命表（Life Table），發現任1美國人活到25歲的機率為0.96716，活到65歲的機率為0.79529，求1個25歲的美國人可以再活到65歲的機率。

P（B∣A）＝ P（A and B）/P（A）＝ 0.79529/0.96716＝0.8223

可用工具：http://www-stat.stanford.edu/~naras/jsm/examplebot.html

第5章 機率分配

分佈（Distribution）就是各個數值出現的次數或頻率。

凡隨機�Z數為機率，其出現機率與樣本空間之函數對映關係，稱為機率分配函數。

若為非連續性、只有2種類別的有限母群體，抽出不放回方式重複抽取樣本，可用超幾何分配計算：

N所有樣本數（母群體）; R含某種性質樣本數; k 被抽出的樣本數；x為抽出樣本中含某性質的樣本數； 「C代表組合函數，算法為C（R,x）＝R！/x！【R-X】！」則：

f(x) = C(R,x)*C(N-R, k-x) / C(N,k)

例：假設某袋內有10個球，8白2黑，若由其中抽出5個，抽到1個黑球的機率為何？

N＝10，R＝2，k＝5，x＝1，

可以用計算機算，或用Microsoft Excel。

選Microsoft Excel中f（x）項之HYPGEOMDIST函數，在Sample_s項（樣本中成功之個數），填1；在Number_sample（所抽樣本總數）項，填5；在Populations項（母體中含此黑色特性之個體總數），填2；在Number_pop項（母體共有多少個體總數），填10。則答案立即算出為0.555555556。

練習用Excel以外之任1免費軟體計算此題，並將步驟、結果以e-mail至教師信箱。2%

若實驗的結果只有2種類別（男、女；正、反；合格、不合格；…），由1個無限母群體中抽取N個樣本， r為成功次數。則可用二項分配求其機率為：其中π代表任何1次實驗中事件成功的機率。

若乃以前例：假設某袋內有10個球，8白2黑，若採抽出放回方式，由其中抽出5個，抽到1個黑球的機率為何？

由於抽出放回，故母群體為∞。且每次抽到黑球的機率π＝2/10＝0.2；N＝5；r＝1；

可以用計算機算，或用Microsoft Excel。

選Microsoft Excel中f（x）項之BINOMDIST函數，在Number_s項（實驗成功之次數），填1；在trials（實驗次數）項，填5；在Probability_s項（每次實驗成功之機率），填0.2；在Cumulative項（代表是否要連續成功，是則填True，否則填false），因只要1有次成即可，即使超過1次也無關連續與否，故填false。則答案立即算出為0.4096。

練習用Excel以外之任1免費軟體計算此題，並將步驟、結果以e-mail至教師信箱。2%

或用：Exact Binomial Probability Calculator：

http://faculty.vassar.edu/lowry/webtext.html

在N項填5，K項填1，P項填0.2，再點Calculate即得結果。

若是二項分配每次實驗成功之機率很小時，法國數學家S.D. Poisson研究出Poisson分配：（ http://episte.math.ntu.edu.tw/articles/sm/sm_16_07_1/index.html , http://rockem.stat.sc.edu/prototype/calculators/index.php3?dist=Poisson , http://www.anesi.com/poisson.htm , http://www.changbioscience.com/stat/prob.html  ）

若m代表某1特定時空內事件隨機發生的平均數（為1個期望值，即機率乘總個體數），a為實�拑o生次數，e為自然對數之底（e ＝2.718）則 ：

例：注射某疫苗有不良反應的機率為0.001，求2000人中（A）恰有3人，（B）超過2人，注射該疫苗後有不良反應之機率。

（A）   a＝3；m＝0.001 x 2000＝2

用Microsoft Excel：選Poisson：

在x項（實際發生數），填3；在Mean項（即m值），填2；在Cumulative項填false，即得0.1804。

（B）   a>2『即求1-P（0）-P（1）-P（2）之值』

比照（A）計算。

練習用Excel以外之任1免費軟體計算此題，並將步驟、結果以e-mail至教師信箱。2%

練習：5選1的選擇題，答對2分，答錯倒扣1分，對不會做的題目，猜或不猜？2%

而自然界連續隨機變數，則多近似常態分配：

式中

 為母群體平均數， 為母群體�Z異數，π是圓周率＝3.1416，e是自然對數底，y是連續隨機變數。由於每1組μ及σ就有1條常態分配曲線，很複雜，故常用標準常態分配：

標準常態分配：

將常態分配以0點為中心，標準差為1的，定為標準常態分配。

常態分配可換算為標準常態分配：令

Z的意義為，原變數y距誰平均數μ有幾個標準差。

看動畫：http://huizen.dds.nl/~berrie/normal.html

在常態分配圖中

μ+/- 1σ 占68.27%面積

μ+/- 2σ 占95.45%面積

μ+/- 3σ 占99.73%面積

例：假設成年女子身高呈常態分配，μ＝160cm，σ＝5cm，試求（A）身高矮於165cm者占？%？（B）身高高於165cm者占？%？

（A）.使用Microsoft Excel；用Standardize函數；在X項填165，在Mean項填160，在Standard_dev項填5，得Z值為1。然後，再用NORMSDIS函數，在Z項填入1，得值0.8413。

（B）.1-0.8413＝0.1587

或用z to P Calculator ： http://faculty.vassar.edu/lowry/ch6apx.html 

練習：假設某校某班的普通生物學成績如下：

趙79 錢86 孫45 李66 鄭90 吳54 周77 主83 馮76 陳69 呂74 衛89 張65 柳72 宋98 馬37 劉88 公孫47 關80 何70 楊57

請以標準化常態分配，將此班同學成績換算為A、A-、B+、B、B-、C+、C、C-、D+、D、D-、…的成績，並說明之。並請論在同校中，使用此種評分制，與百分制之優劣？在不同校中比較又如何？（要列述出演算過程，或利用Excel或其它免費軟體之步驟）。2%。

練習：假設臺東大學20歲同學平均舒張血壓為80mmHg，標準差為8mmHg，若隨機由臺東大學20歲同學中抽64人為樣本，求：

1.    樣本平均數的標準差為何？

2.    樣本平均數大於82mmHg之機率？

3.    如樣本改為16人，其樣本平均數大於82mmHg之機率？

4.    若隨機由臺東大學20歲同學中抽1人為樣本，其血壓大於82mmHg之機率？

5.    在抽64人為樣本時，理論上有多少人血壓大於82mmHg？2%。（要列述出演算過程，或利用Excel或其它免費軟體之步驟）

練習：1種全身麻醉劑，能達成外科麻醉所需劑量因人而異，其分配為常態，μ₁＝50mg，σ₁＝10mg，此麻醉劑致死量也近常態，μ₂＝120mg，σ₂＝20mg。若某1劑量恰能使95%患者麻醉，請問，會有多少百分比患者可能因過量而死亡？2%。（要列述出演算過程，或利用Excel或其它免費軟體之步驟）

測驗題：設SARS死亡率為0.002，求2000人中少於5人因此疾死亡之機率。2%

測驗題：某�W院某一年內共接生100活產嬰兒，其中53名男嬰平均體重3,250g，標準差250g，47名女嬰，平均體重3,080g，標準差240g，在95%信賴水準，請估全國男女新生嬰兒之平均體重。2%

第6章 單1母群體平均數的估計及檢定

抽樣分配是統計推論的基礎。可用樣本統計量來推論母群體的�趧ヾC

在某一信賴程度內，由樣本統計量所求出預期可包括母群體�趧う瑤d圍，稱為信賴區間（Cofidence Interval-CI）。

信賴水準（cofidence level），指推論者有？%（如95%、99%）的信心，所推論的母群體的�趧ヾA會在某信賴區間內。

在大多數研究中，大樣本不經濟，多以小樣本（n<30）資料推估出母群體資料。英國學者Gosset研究出推估母群體標準差之法，並以Student筆名發表，將�Z量設為t。故稱t分配或學生分配。（http://mathworld.wolfram.com/Studentst-Distribution.html ）

 式中，n代表樣本數，μ代表母群體平均數，  代表樣本平均數， s 代表樣本標準差，它的自由度為n-1。

t分配與常態分配的關係，可�謔牷Ghttp://www.econtools.com/jevons/java/Graphics2D/tDist.html 。

當n>30時，t分配已接近常態分配，可用常態分配推估。

t分配與母群體平均數μ的信賴區間推估：

令α為1-信賴水準（即1-0.95或1-0.99），若母群體標準差σ已知則：

樣本平均數-t_α/2σ<μ<樣本平均數+ t_α/2σ

若母群體標準差σ未知，則用σ＝s/√n

樣本平均數-t_α/2 s/√n <μ<樣本平均數+ t_α/2 s/√n

例：

某�W師給16位嬰兒吃某新添加食品，1個月後，體重增加量為448、229、316、105、516、496、130、242、470、195、389、97、458、347、340、212（g）。求95%信心水準下之嬰兒體重增加量的信賴區間。

先用Microsoft Excel求出平均數為311.9g，及標準差s＝142.8g

α＝0.05，

用Microsoft Excel之TINV選項。在Probability項，填0.05；在Deg_Freedom項，填15，得2.131。此為t值。

再用公式：樣本平均數-t_α/2 s/√n <μ<樣本平均數+ t_α/2 s/√n

s/√n＝142.8/√16＝76.1（可用http://www.df.lth.se/~mikaelb/pocketcalc.shtml 之網上計算機算）代入上式得：

311.9-76.1＜μ< 311.9+76.1è235.8＜μ＜388.0（g）

各種機率分配值，亦可�謔牷Ghttp://stat-www.berkeley.edu/~stark/SticiGui/Text/index.htm

第7章 假設檢定

以樣本資料來對母群體下決策。

要下決策，需先對母群體做假設。並設法推翻此假設。由於此假設有被否定的命運，故稱虛無假設（Null Hypothesis），以H₀代表。另1對立假設（Alternative Hypothesis），則為H₁。

對對單1樣本而言，若假設為H₀：μ＝μ₀ （http://www.cas.lancs.ac.uk/glossary_v1.1/hyptest.html#hypothtest）

則有3種可能：

第I及II型錯誤，可�謔牷Ghttp://www.pinkmonkey.com/studyguides/subjects/stats/chap8/img11.gif

第I型（α）錯誤為H₀為真卻拒絕假設。第II型（β）錯誤為H₀為做卻接受假設。

顯著水準（Significant Level）為決策者願冒犯第I型錯誤的機率。通常用α表示。如α＝0.05即100次中有可能5次犯錯。

統計上有2種計算方式，��尾檢定，或單尾檢定，依狀�G而定。

�謔牷Ghttp://www.stat.sc.edu/~ogden/javahtml/power/power.html

若檢定虛無假說為假，用雙尾檢定（各尾占α/2）。若檢定虛無假說在某一方向假，用單尾檢定（α）。可是Chi-test、F-test、t-test常用單尾。

例：假設正常人血蛋白含量平均為7.25（太高太低均不宜），某人連續8天，測得其血蛋白含量為7.23、7.25、7.28、7.29、7.32、7.26、7.27、7.24，以0.01顯著水準，判斷該員血蛋白含量是否正常。

小樣本，故用t分配。

先用Microsoft Excel，算出樣本平均數為7.2675，樣本標準差為0.0292，s/√n＝0.0292/√8＝0.0103

再用公式： 求出t₀值為（7.2675-7.25）/0.0103＝1.7

立假設：

H₀：μ＝7.25

H₁：μ≠7.25

因檢定≠或＝，故為��尾檢定。但為t-test（屬Chi、F、t、3者多用單邊），乃以α計算。

df＝8-1＝7

用Microsoft Excel之TINV選項。在Probability項，填0.01（α）；在Deg_Freedom項，填7，得±3.499。此為t值。

經比較3.499＞1.7，故不能拒絕假設。表示，該員可判為正常。

練習：

假設養殖池中，每ml之平均含菌量在70個以下時，方為合格。現於某養殖池中抽取9處樣本，含菌數為：69 74 75 70 72 73 71 73 68，在α＝0.05下，該池是否合格？

假設  H₀：μ≦70

H₁：μ＞70

只有9個樣本，用t分配，單邊檢定，

df＝8

用Microsoft Excel，TDIS，在X項將9個樣本值輸入，再填入df＝8，並選單邊＝1，得p值為1.21735E-12（1.21735 x 10^-12），此機率太小，表示μ≦70的機率太小，不成立。

例：學生20人生物某次測驗成績為：

72     69     98     87    

78     76     78     66

85     97     84     86

88     76     79     82

82     91     69     74

教師想知道，此成績與全校學生生物之平均76有無差異？

The degrees of freedom for t is equal to the degrees of freedom for the estimate of which is N-1 = 20 - 1 = 19. A t table can be used to calculate that the two-tailed probability value of a t of 2.44 with 19 df is .025.

5. The probability computed in Step 4 is compared to the significance level stated in Step 2. Since the probability value (.025) is less than the significance level (.05) the effect is statistically significant.

6. Since the effect is significant, the null hypothesis is rejected. It is concluded that the mean reading achievement score of children in the city in question is higher than the population mean.

7. A report of this experimental result might be as follows:

The mean reading-achievement score of fifth grade children in the sample (M = 80.85) was significantly higher than the mean reading-achievement score nationally (µ = 76), t(19) = 2.44, p = .025.

The expression "t(19) = 2.44" means that a t test with 19 degrees of freedom was equal to 2.44. The probability value is given by "p = .025." Since it was not mentioned whether the test was one- or two- tailed, a two-tailed test is assumed.

樣本大小之決定：

令誤差值為±d，誤差即為信賴區間，故±d＝±Z_α/2σ/√nè n＝（Z_α/2σ/d）²

例：假設某國5年前調查成年女子平均身高為155cm，標準差為5cm，現以95%信賴水準，想再調查成年女子平均身高，且希望誤差在±1cm內，要抽多少樣本？

σ＝5，d＝±1，α＝1-0.95＝0.05，

使用Microsoft Excel之NORMSINV項，在Probability項，填α/2＝>即0.025，得Z_α/2＝-1.96，採正值。

n＝「（1.96x 5）/1」²＝96.04è97（人）

練習：某減肥廣號稱「4個月減20公斤」，經抽取25個顧客，發現平均減15公斤，標準差為5.5公斤，此廣告是否可靠？2%

第8章 �O個母群體平均數差的估計與檢定

可分獨立樣本與成對樣本2類。依樣本大小（30以上或以下）直接用常態分配或t分配來估檢。

例：2組老鼠，分別飼以不同品牌飼料，並於第84天分別量體重，如下：

甲牌組：134 146 104 119 124 161 107 83 113 129 97 123

乙牌組：70 118 101 85 107 132 94

若以95%顯著水準，比較此2品牌飼料有無差異？

獨立樣本。

立假設：

H₀：μ₀＝μ₁

H₁：μ₀ ≠μ₁

使用Microsoft Excel，在工具項，選「資料分析」，再選「t檢定：2個母群體平均數差的檢定，假設變異數相等」項，再將上述甲、乙組體重填入Test-2之Sheet6格中，再將變數1、2的範圍填入，在假設的均數差項填0（因H₀：μ₀＝μ₁），在α項，填0.05，並指定輸出位置，再點確定即得Sheet6之結果如下：

df＝2組個數和-2

由於2.1098＞1.8914，故接受假設，即2品牌無差異。

試用另1種免費軟體做此題。例出步驟2%。

例：5位病人至�W院注射某藥後低血壓�Z化如下：

注射前mmHg 97 85 87 97 71

注射後      100 94 98 96 88

若以99%顯著水準，此些病人注射前後，血壓有無改變？

成對資料。

立假設：

H₀：μ₀＝μ₁

H₁：μ₀ ≠μ₁

以Microsoft Excel；資料分析；用「t 檢定：成對母體平均數差異檢定」，將資料填入，得：

由於5.8408＞2.4054，故接受假設，即血壓無差異。

df＝1組之個數-2（因成對資料）

練習：2位同�a分別計算同一批細菌培養皿上菌群數，得下列結果：

甲 139 121 39 163 191 61 179 218 297 165 91 92

乙 191 181 67 143 234 80 250 239 289 201 80 99

若以99%信賴範圍計，此2人之結果有無差別？3%。

測驗：

某減肥法�\稱，平均每2週可減體重5公斤，7位婦女�諝[2週後，體重記錄為：

前 58.5 60.3 61.7 69 64 62.6 56.7（kg）

後 60 54.9 58.1 62.1 58.5 59.5 54.4

假設體重近常態分配，請用5%顯著水準檢定此減肥法是否如其所稱之有效？3%

測驗：某醫生�\稱發明治SARS新藥，並以某種動物實驗，結果動物存活月數為：

接受新藥治療者  2.1   5.3    1.4   4.6   0.9

未接受新藥治療者  1.9    0.5    2.8    3.1

請問，此藥效如何？3%。

The question is whether the difference between the means of these two groups of subjects is statistically significant.

1. The first step is to specify the null hypothesis and an alternative hypothesis. For experiments testing differences between means, the null hypothesis is that the difference between means is some specified value. Usually the null hypothesis is that the difference is zero.

For this example, the null and alternative hypotheses are:

H_o: µ₁ - µ₂ = 0
H₁: µ₁ - µ₂ 0

2. The second step is to choose a significance level. Assume the .05 level is chosen.

3. The third step is to compute the difference between sample means (M_d). In this example, M_t = , M_N = and M_d = MT - M_N = .

4. The fourth step is to compute p, the probability (or probability value) of obtaining a difference between and the value specified by the null hypothesis (0) as large or larger than the difference obtained in the experiment. Applying the general formula,

where M_d is the difference between sample means, µ₁ - µ₂ is the difference between population means specified by the null hypothesis (usually zero), and is the estimated standard error of the difference between means.

The estimated standard error, , is computed assuming that the variances in the two populations are equal. If the two sample sizes are equal (n₁ = n₂) then the population variance s² (it is the same in both populations) is estimated by using the following formula:

MSE = ( + )/2

where MSE (which stands for mean square error) is an estimate of s². Once MSE is calculated, can be computed as follows:

where n = n₁ = n₂. This formula is derived from the formula for the standard error of the difference between means when the variance is known.

5. The probability computed in Step 4 is compared to the significance level stated in Step 2. If the probability value (  ) is less than the significance level (.05) the effect is significant.

6. Science the effect is significant, the null hypothesis is rejected. It is concluded that the mean memory score for experts is higher than the mean memory score for novices.

7. A report of this experimental result might be as follows:

The mean number of pieces recalled by tournament players (M_t =    ) was significantly higher than the mean number of pieces recalled by novices (M_t =    ), t(    ) =    , p =     .

The expression "t(    ) =     " means that a t test with    degrees of freedom was equal to     . The probability value is given by "p =    ." Since it was not mentioned whether the test was one- or two-tailed, it is assumed the test was two tailed.

Unequal Sample Sizes
The calculations in Step 4 are slightly more complex when n₁ n₂. The first difference is that MSE is computed differently. If the two values of s² were simply averaged as they are for equal sample sizes, then the estimate based on the smaller sample size would count as much as the estimate based on the larger sample size. Instead the formula for MSE is:

MSE = SSE/df

where df is the degrees of freedom (n₁ - 1 + n₂ - 1) and SSE is: SSE = SSE₁ + SSE₂
SSE₁ = (X - M₁)² where the X's are from the first group (sample) and M₁ is the mean of the first group. Similarly, SSE₂= (X- M₂)² where the X's are from the second group and M₂ is the mean of the second group.

The fomula: MSE = ( + )/2 cannot be used without modification since there is not one value of n but two: (n₁ and n₂). The solution is to use the harmonic mean of the two sample sizes. The harmonic mean (n_h) of n₁ and n₂ is:
The formula for the estimated standard error of the difference between means becomes:

The hypothetical data shown below are from an experimental group and a control group.

3

5

7

7

8

3

4

6

7

n₁ = 5, n₂ = 4, M₁ = 6, M₂ = 5, SSE₁ = (3-6)² + (5-6)² + (7-6)² + (7-6)² + (8-6)² = 16, SSE₂ = (3-5)² + (4-5)² + (6-5)² + (7-5)² = 10

SSE = SSE₁ + SSE₂ = 16 + 10 = 26
df = n₁ - 1 + n₂ - 1 = 7
MSE = SSE/df = 26/7 = 3.71

The p value associated with a t of 0.77 with 7 df is .47. Therefore, the difference between groups is not significant.

Summary of Computations
1. Specify the null hypothesis and an alternative hypothesis.
2. Compute M_d = M₁ - M₂
3. Compute SSE₁ = (X - M₁)² for Group 1 and SSE₂ = (X - M₂)² for Group 2
4. Compute SSE = SSE₁ + SSE₂
5. Compute df = N - 2 where N = n₁ + n₂
6. Compute MSE = SSE/df

7. Compute: (If the sample sizes are equal then n_h = n₁ = n₂).
8. Compute:

9. Compute:

where µ₁ - µ₂ is the difference between population means specified by the null hypothesis.
10. Use a t table to compute p from t (step 9) and df (step 5).

Assumptions
1. The populations are normallly distributed.
2. Variances in the two populations are equal.
3. Scores are independent (Each subject provides only one score)
See also: Confidence interval on µ₁ - µ₂, independent groups, s estimated

信賴區間：

Following the general formula for a confidence interval, the formula for a confidence interval on the difference between means ( M₁ - M₂) is:
M_d (t)()
where M_d = M₁ - M₂ is the statistic and is an estimate of (the standard error of the difference between means). t depends on the level of confidence desired and on the degrees of freedom. The estimated standard error, , is computed assuming that the variances in the two populations are equal. If the two sample sizes are equal (n₁ = n₂) then the population variance s² (it is the same in both populations) is estimated by using the following formula:
MSE = ()/2
where MSE (which stands for mean square error) is an estimate of s². Once MSE is calculated, can be computed as follows:
=

A concrete example should make the procedure for computing the confidence interval clearer. Assume that an experimenter were interested in computing the 99% confidence interval on the difference between the memory spans of seven- and nine-year old children. Four children at each age level are tested and their memory spans are shown below:
The first step is to compute the means of each group: M_{Age 7} = 3.75 and M_{Age 9} = 6.00. Therefore, M_d = 3.75 - 6.00 = -2.25. To obtain a value of t, one must first compute the degrees of freedom (df). The degrees of freedom is equal to the degrees of freedom for MSE (MSE is used to estimate s²). Since MSE is made up of two estimates of s² (one for each sample), the df for MSE is the sum of the df for these two estimates. Therefore, the df for MSE is (n -1) + (n - 1) = 3 + 3 = 6.

the df for MSE is (n -1) + (n - 1) = 3 + 3 = 6. A t table shows that the value of t for a 99% confidence interval for 6 df is 3.707. The only remaining term is s_Md .
The first step is to compute and :
= .917 and = .667.
MSE = (.917 + .667)/2 = .792. From the formula:
==

= .629

All the terms needed to construct the confidence interval have now been computed. The lower limit (LL) of the interval is:
LL = M_d - t
= -2.25 - (3.707)(.629)
= -4.58.

UL = -2.25 + (3.707)(.629) = .09.
Therefore -4.58 ≤ m₁ - m₂ ≤ 0.09.

The calculations are only slightly more complicated when the sample sizes are different (n₁ does not equal n₂). The first difference in the calculations is that MSE is computed differently. If the two values of s² were simply averaged as they are in the case of equal sample sizes, then the estimate based on the smaller sample size would count as much as the estimate based on the larger sample size. Instead the formula for MSE is:

MSE = SSE/df

where df is the degrees of freedom and SSE is the sum of squares error and is defined as:

SSE = SSE₁ + SSE₂
SSE₁ =

where the X's are from the first group (sample) and M₁ is the mean of the first group. Similarly,

SSE₂=

where the X's are from the second group and M₂ is the mean of the second group.

The formula =cannot be used without modification since there is not one value of n but two: (n₁ and n₂).

The solution is to use the harmonic mean of the two sample sizes for n. The harmonic mean (n_h) of n₁ and n₂ is:


Therefore the formula for the estimated standard error of the difference between means is:

For the example of the confidence interval on the difference between memory spans of seven-year olds and nine-year olds, assume that one more seven year old was tested and the resulting memory span score was 3. For these data, M₁ = 3.6, M₂ = 6.0, and M_d = -2.4
SSE₁ = (3-3.6)²+(3-3.6)²+(3 - 3.6)² + (4 - 3.6)² + (5 - 3.6)² = 3.2.
SSE₂ = (5-6)²+(6-6)²+(6-6)²+(7-6)²= 2.0.

Therefore SSE = 3.2 + 2.0 = 5.2. The df are equal to the sum of the df for and which is 4 + 3 = 7. Since MSE = SSE/df,

MSE = 5.2/7 = .743.

The harmonic mean of the n's is:


= 2/(.2 + .25) = 4.4444.


= .578.

Finally, a t table can be used to find that the value of t (with 7 df) to be used for the 99% confidence interval is 3.499.

The confidence interval is therefore:

LL = -2.4 - (3.499)(.578) = -4.42 UL = -2.4 + (3.499)(.578) = -0.38
-4.42 µ₁ - µ₂ -.38

Summary of Computations
1. Compute M_d = M₁ - M₂
2. Compute SSE₁ = (X - M₁ )² for Group 1 and SSE₂ = (X - M₂ )² for Group 2
3. Compute SSE = SSE₁ + SSE₂
4. Compute df = N - 2 where N = n₁ + n₂
5. Compute MSE = SSE/df
6. Find t from a t table.
7. Compute (If the sample sizes are equal then n_h = n₁ = n₂).
8. Compute
9. Lower limit = M_d - t
10. Upper limit = M_d + t
11. Lower limit µ₁- µ₂ Upper limit


Assumptions:
1. The populations each are normally distributed.
2. (Homogeneity of variance)
3. Scores are sampled randomly and independently from 2 different populations

第9章 卡方檢定（Chi-square Test）

常用於檢測2間斷變數間的關�m性。即實際次數與理論次數是否相同。

例：用3種藥分別各對咳嗽病人治療，3天後結果如下：

藥品        甲       乙       丙

有效        70      160      168（人）398

無效        30       40       32      102

合計        100      200      200      500

在α＝0.01下，檢定3種藥效果是否相同？

398/500＝0.796為期望比，用此比求出期望值：

藥品        甲       乙       丙

有效        79.6      159.2     159.2人）398

無效        20.4      40.8      40.8      102

合計        100      200      200      500

df＝（行數-1）x（列數-1）

用Microsoft Excel，由fx選CHITEST項，分別將實�怑�與期望值表填入，即得。見Test-2之Sheet7。值為0.0176＞0.01，故接受3種藥效果相同。

試用不同軟體做此題（如http://graphpad.com/quickcalcs/index.cfm ），列出步驟。2%

Empirical Approximation of a Chi-Square Sampling Distribution

   

Theoretical Sampling Distribution of Chi-Square (df=2)

   

Chi-Square Sampling Distributions for df=2, 3, and 4

   

第10章 母群體變異數的估計與檢定

前曾在「兩個母體平均數差的檢定時，假設變異數相等」。但兩個母體變異數是否相等，要用F分配加以檢定。

F＝「（Chi₁）²/df₁」÷「（Chi₂）²/df₂」

而棄卻區為：

H₀          H₁          棄卻區

σ₁²＝σ₂²   σ₁²≠σ₂²             F＝S₁²/ S₂² ＞F_α/2，n₁－1，n₂－1

                        or F＝S₁²/ S₂²＜F_α/2，n₁－1，n₂－1

σ₁²≦σ₂²   σ₁²＞σ₂²             F＝S₁²/ S₂² ＞F_1－α，n₁－1，n₂－1

σ₁²≧σ₂²   σ₁²＜σ₂²             F＝S₁²/ S₂² ＜F_α，n₁－1，n₂－1

可用Microsoft Excel 中fx之FTEST項。亦可�謔牷Ghttp://darwin.eeb.uconn.edu/simulations/jdk1.0/wahlund.html

例：某藥廠擬購裝瓶機，每瓶內之�Z異乃機器良窳之重要因素，今由A牌機器抽30瓶產品，得S_A²＝0.027，由B牌機器S_B²＝0.065，若α＝0.05，可否認為A牌機器優於B牌機器？

假設H_{0  ：} σ₁²≦σ₂²   H_{1  ：} σ₁²＞σ₂²            F＝S₁²/ S₂² ＞F_1－α，n₁－1，n₂－1

F＝（0.027/29） ÷（0.065/9）＝1.29

由Excel之FINV項，將Probability項填0.95，df1項填29，df2項填9，得0.4499，而1.29＞0.4499，故接受假設。即認為A牌機器優於B牌機器。

有時必須檢定2個以上母群體之平均數是否相等，可用變異數分析（Analysis of Variance--ANOVA）。

又分單因子變異數分析（Single factor analysis of varance）、2因子變異數分析（Two factor analysis of varance）（又分不考慮2因子間交互影�遄A與考慮2因子間交互影�鉞�2種「在本課不述」）、及多因子變異數分析（Multi- factor analysis of varance）（在本課不述）。

單因子變異數分析之例；25位病人，分5組，每人服用1種廠牌退燒藥後，之退燒時數：

藥     A    B    C    D    E

5    9    3    2    7

4    7    5    3    6

8    8    2    4    9

6    6    3    1    4

3    9    7    4    7

Total   26   39   20   14   33

平均   5.2  7.8   4.0   2.8  6.6

在0.05顯著水準，用變異數分析法檢定5種廠牌退燒藥，持續退燒時間相等的假設。（注意：資料偶有缺亦可算）

假設：H₀ ：μ₁＝μ₂＝μ₃＝μ₄＝μ₅         H₁ ：至少有2個μ不相等

      而F＝S₁²/ S₂²

用Excel，在工具項，選資料分析，再選單因子變異數分析，再將資料填入，即得：

因F＞2.866，故拒絕假設。

試用不同軟體做此題3%。列出步驟。

測驗：

檢測4種廠牌同種針劑之主成份含量（μg）：

樣本

廠牌      1       2        3         4

A       9.3       9.4      9.6        10

B       9.4       9.3      9.8        9.9

C       9.2       9.4      9.5        9.7

D       9.7       9.6      10       10.2

若α＝0.05，請問，此4廠牌平均成份是否相同？用2種不同軟體解題。4%

另例：見Test-3，Sheet1。

測驗：

4個實驗室進行同項生化分析，結果：

Lab.  A      B     C      D

58.7     62.7    55.9    60.7

61.4     64.5    56.1    60.3

60.9     63.1    57.3    60.9

59.1    59.2    55.2    61.4

58.2    60.3    58.1    62.3

若α＝0.05，求這些實驗室的結果是否相符？3%

測驗：

下表為5位國立台東大學某系某班學生4科成績：

                    科目

            生統         分生        遺傳        生資

學生

張xx         68          57           73          61

李xx         83          94           91          86

王xx         72          81           63          59

趙xx         55          73           77          66

吳xx         92          68           75          87

若α＝0.05，求（1）這些課難度是否相同？

（2）學生能力是否相等？4%

不考慮2因子間交互影�鄐�2因子變異數分析：

3種小麥品種，在施用4種肥料下，之單位面積產量（kg）：

品種

              A       B        C

肥料

甲            64       72       74

乙            55       57        47

丙            59       66        58

丁            58       57        53

在α＝0.05下，小麥品種，與肥料種類，對平均產量有無影�遄H

假設H₀ ：α₁＝α₂＝α₃＝0（列效果為0）       H₁ ：至少有1個α_i不相等

H₀’：β₁＝β₂＝β₃＝0（行效果為0）       H₁’：至少有1個β_j不相等

使用Excel，工具項＝＞雙因子變異數分析無重複試驗＝＞代入資料得：

其中9.22＞4.76故拒絕H₀，即肥料�N影響產量。而1.56＜5.14故接受H₀^’，即品種不�N影響產量。

第11章 迴歸（regression）與相關（Correlation）

迴歸是由英國生物學家Galton（1877）研究人類身高與父母親身高所創用的名詞。身高很高的父親，兒子會比父親略矮，很矮的的父親，兒子會比父親略高。這種身高會跑回（going back）平均數的現像，稱之。在散佈圖上符合此資料分佈情況的線段，稱「迴歸線」，表示此線的方程式稱「迴歸方程式-regression equation」。以後推廣至凡用於估計線或方程式的統計技術均稱「迴歸分析」。

最簡單的為直線迴歸：一般均用最小平方法（Least square method）

相關係數（Correlation Coefficient）：資料量大，r＜-0.7或r＞0.7則表示2�Z數有相關。

可用Excel http://www.gifted.uconn.edu/Siegle/research/Correlation/excel.htm or http://www.changbioscience.com/stat/corr.html , http://fonsg3.let.uva.nl/Service/Statistics/Correlation_coefficient.html , http://www.ifigure.com/math/stat/regress.htm 軟體。

The correlation between two variables reflects the degree to which the variables are related. The most common measure of correlation is the Pearson Product Moment Correlation (called Pearson's correlation for short). When measured in a population the Pearson Product Moment correlation is designated by the Greek letter rho (r). When computed in a sample, it is designated by the letter "r" and is sometimes called "Pearson's r." Pearson's correlation reflects the degree of linear relationship between two variables. It ranges from +1 to -1. A correlation of +1 means that there is a perfect positive linear relationship between variables. The scatterplot shown on this page depicts such a relationship. It is a positive relationship because high scores on the X-axis are associated with high scores on the Y-axis.

A correlation of -1 means that there is a perfect negative linear relationship between variables. The scatterplot shown to the right depicts a negative relationship. It is a negative relationship because high scores on the X-axis are associated with low scores on the Y-axis. A correlation of 0 means there is no linear relationship between the two variables.

The second graph shows a Pearson correlation of 0.
Correlations are rarely if ever 0, 1, or -1. Some real data showing a moderately high correlation are shown ：

The scatterplot below shows arm strength as a function of grip strength for 147 people working in physically-demanding jobs (click here for details about the study).The plot reveals a strong positive relationship. The value of Pearson's correlation is 0.63.

Other information about Pearson's correlation can be obtained by clicking one of the following links:

• Computational formula
• Sampling distribution
• Confidence interval
• Confidence interval on difference between r's

The experiment shows that there is still uncertainty about the difference in correlations. It could be that the correlation for females is as much as 0.49 higher; but it could also be 0.15 lower.

Summary of Computations
1. Compute the sample r's.
2. Use an r to z' table to convert the values of r to z'.
3. Compute z'₁ - z'₂.
4. Use a to z table to find the value of z for the level of confidence desired.
5. Compute:

6. Lower limit = z'₁ - z'₂ - (z)()
7. Upper limit = z'₁ - z'₂ + (z)()
8. Use an r to z' table to convert the lower and upper limits to r's.

Assumptions:
1. Each subject (observation) is sampled independently from each other subject.
2. Subjects are sampled randomly.
3. The two correlations are from independent samples (different groups of subjects). If the same subjects were used for both correlations then the assumption of independence would be violated.

第12章 無母數統計（Nonparametric Methods）

例：下為12位病人等診時間（min）：

17 15 20 20 32 28 12 26 25 25 35 24若α＝0.05，問，病人平均等診時間是否在20min以內？

H0：u＝20

H1：u＜20

將候診時間＞20者為＋，＝20者為0，＜20者為－，可得：

－－00＋＋－＋＋＋＋＋，0者不計，依二項分配n＝10，X＝3，p＝1/2得p＝0.1719＞0.05，接受假設。即u不小於20min。

測驗：

某次生統考試，有是非20題，正確答案為：

○       ××○×○×○○×○××○×○×○○×

問，此是非題的安排是否隨機？

、